BAB I
PENDAHULUAN
Dalam
kehidupan sehari-hari, sering kita jumpai banyak hal yang dapat kita
deskripsikan dalam bentuk data. Informasi data yang diperoleh tentunya diolah
terlebih dahulu menjadi sebuah data yang mudah dibaca dan dianalisa. Statistik
adalah ilmu yang mempelajari cara-cara pengolahan data. Untuk memperoleh
data-data tersebut, diperlukan adanya suatu penelitian.
Mean, Median, Modus sama-sama merupakan ukuran
pemusatan data yang termasuk kedalam analisis statistika deskriptif. Namun,
ketiganya memiliki kelebihan dan kekurangannya masing-masing dalam menerangkan
suatu ukuran pemusatan data. Untuk tahu kegunaannya masing-masing dan kapan
kita mempergunakannya, perlu diketahui terlebih dahulu pengertian analisis
statistika deskriptif dan ukuran pemusatan data. Analisis Statistika deskriptif
merupakan metode yang berkaitan dengan penyajian data sehingga memberikan
informasi yang berguna. Upaya penyajian ini dimaksudkan untuk mengungkapkan
informasi penting yang terdapat dalam data ke dalam berntuk yang lebih ringkas
dan sederhana yang pada akhirnya mengarah pada keperluan adanya penjelasan dan
penafsiran (Aunudin, 1989).
1.
Apa
yang dimaksud dengan Modus?
2.
Bagaimana
penyelesaian
Modus dari Data Tunggal dan Data Kelompok?
3.
Bagaimana
Penggunaan Modus?
4.
Apa sajakah Kelebihan dan Kelemahan Modus?
1.
Dapat
mengetahui pengertian dari Modus.
2.
Dapat
menyelesaikan perhitungan Modus dari Data Tunggal dan Data
Kelompok
3.
Dapat
mengetahui Penggunaan Modus
4.
Dapat
mengetahui
Kelebihan dan Kelemahan Modus
PEMBAHASAN
Modus adalah skor yang paling sering
muncul di dalam distribusi. Dalam istilah umum, kata modus atau mode
berarti “bentuk yang lazim” atau “gaya yang terkenal”. Modus merupakan
ukuranyang sangat berguna untuk tendensi sentral karena bisa digunakan untuk
menentukan tipe atau nilai rata-rata untuk skala pengukuran, termasuk skala
nominal. Pada statistik modus
atau mode dapat diartikan sebagai gejala atau nilai yang paling sering
muncul atau paling banyak muncul. Pada data yang sudah dibuat dalam distribusi
frekuensi, maka modus adalah interval kelas (biasanya diwakili oleh
titik tengahnya) yang memiliki frekuensi paling banyak. Berkaitan dengan notasi
atau lambing, modus tidak memiliki notasi khusus. Notasi yang sering digunakan
untuk modus adalah Mo.
Pada
distribusi suatu data hanya akan ditemukansatu rata-rata hitung (mean)
dan satu median. Akan tetap untuk modus pada suatu distribusi
data dimungkinkan untuk ditemukan lebih dari satu modus. Mengingat ada
kemungkinan terdapat dua atau lebih skor yang mempunyai frekuensi sama-sama
paling besar. Dalam grafik distribusi frekuensi, modus yang berbeda akan
terlihat jelas, mempunyai puncak tertinggi yang sama. [1]
Modus adalah nilai data yang paling sering muncul atau nilai data
yang frekuensinya paling besar. Data yang belum dikelompokkan bisa memiliki
satu modus, dua modus, atau mungkin tidak mempunyai modus. Data yang memiliki
satu modus disebut monomodus, sedangkan data yang memiki dua modus
disebut bimodus.[2]
Mencari modus untuk data tunggal dapat dilakukan dengan mudah dan
cepat sekali, yaitu hanya dengan memeriksa (mencari) mana di antara skor yang
ada, yang memiliki frekuensi paling banyak. Skor atau nilai yang memiliki
frekuensi paling banyak itulah yang kita sebut modus.
Contoh 1:
Tentukan modus dari data berikut ini!
5,7,7,6,8,6,6,5,8,6
Jawab:
Setelah data diurutkan diperoleh: 5,5,6,6,6,6,7,7,8,8
Modus(Mo) = 6
Contoh 2:
Misalkan data tentang usia 50 orang Guru
Agama Islam yang tercantum pada tabel dapat kita cari modusnya sebagai berikut:
|
Usia (X) |
f |
|
31 30 29 28 M0
(27) 26 25 24 23 |
4 4 5 7 (12)
= f maksimal 8 5 3 2 |
|
Total |
50
= N |
Modus untuk data di atas adalah usia 27
tahun. Mengapa demikian? Sebab dari sejumlah 50 orang Guru Agama Islam
tersebut, yang paling banyak adalah berusia 27 tahun.[3]
2.
Modus dari data yang telah dikelompokkan
Untuk menhitung modus dari data yang telah dikelompokkan
dipergunakan rumus segai berikut:
Keterangan:
Mo= modus
b = batas bawah kelas modus
p = panjang kelas
b1 = frekuensi
kelas modus dikurangi frekuensi kelas sebelumnya
b2 = frekuensi
kelas modus dikurangi frekuensi kelas berikutnya
Contoh:
Tentukan modus dari data berikut!
|
Nilai |
Frekuensi |
|
52
– 58 59
– 65 66
– 72 73
– 79 80
– 86 87
– 93 94
– 100 |
2 6 7 20 8 4 3 |
|
Jumlah |
50 |
Jawab:
Frekuensi terbanyak pada kelas 73 – 79, berarti modusnya terletak pada kelas 73 – 79.
Jadi, modusnya adalah
76,14
Mencari modus kita lakukan apabila kita
berhadapan dengan kenyataan sebagai berikut:
1)
Kita
ingin memperoleh nilai yang menunjukkan aturan rata-rata dalam waktu yang
paling singkat.
2)
Dalam
mencari nilai yang menunjukkan ukuran rata-rata itu kita meniadakan faktor
ketelitian, artinya: ukuran rata-rata itu kita kehendaki hanya bersifat kasar
saja.
3)
Dari
data yang sedang kita teliti (kita cari Modusnya) kita hanya ingin mengetahui
ciri khasnya saja
D. Kelebihan dan Kelemahan Modus
Kelebihan Modus dapat menolong diri kita dalam waktu yang paling
singkat memperoleh ukuran rata-rata yang merupakan ciri khas dari data yang
kita hadapi. Sedangkan kelemahanya ialah kurang teliti karena Modus terlalu
mudah atau terlalu gampang diperoleh (dicapai). Selain itu, jika frekuensi
maksimal yang terdapat dalam distribusi frekuensi data yang kita teliti itu
lebih dari satu buah, maka akan kita peroleh Modus yang banyaknya lebih dari
satu buah. Kemungkinan lainnya, bisa terjadi dalam suatu distribusi frekuensi
tidak dapat kita cari atau tentukan Modusnya, disebabkan karena semua skor yang
ada mempunyai frekuensi yang sama. Jadi sebagai salah satu ukuran rata-rata,
Modus sifatnya labil (tidak stabil).[4]
BAB III
PENUTUP
Modus adalah skor yang paling sering muncul di dalam distribusi. Dalam istilah umum, kata modus atau mode berarti “bentuk yang lazim” atau “gaya yang terkenal”. Modus merupakan ukuranyang sangat berguna untuk tendensi sentral karena bisa digunakan untuk menentukan tipe atau nilai rata-rata untuk skala pengukuran, termasuk skala nominal. Pada statistik modus atau mode dapat diartikan sebagai gejala atau nilai yang paling sering muncul atau paling banyak muncul. Pada data yang sudah dibuat dalam distribusi frekuensi, maka modus adalah interval kelas (biasanya diwakili oleh titik tengahnya) yang memiliki frekuensi paling banyak. Berkaitan dengan notasi atau lambing, modus tidak memiliki notasi khusus. Notasi yang sering digunakan untuk modus adalah Mo.
Sebagai calon pendidik yang masih belajar dan akan mengajarkan terkait statistik pendidikan seharusnya memahami terlebih dahulu mengenai pembelajaran statistik pendidikan supaya pembelajaran berjalan dengan baik dan dapat dipahami.
DAFTAR PUSTAKA
Anas Sudijono. 2015. Pengantar Statistik Pendidikan. Jakarta:
Raja Grafindo
Sopingi. 2015.Pengantar Statistik Pndidikan. Malang:
Gunung Samudra.
Subana;
Rahardi, Moersetyo; dan Sudrajat,
2015. Statistik Pendidikan. Bandung: Pustaka Setia.
 Reviewed by asarisolid
on
7:20 PM
Rating:
Reviewed by asarisolid
on
7:20 PM
Rating:


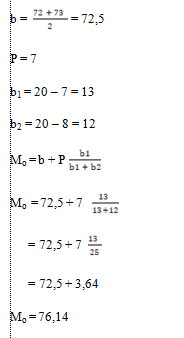
No comments: